I’ve previously posted about our work on quality dimensions for stochastic process models. Process models are ways of describing organisational behaviour, and quality metrics are ways of understanding how well that is represented in the mathematical abstractions called process models. We investigated how quantitative measures behave in an experimental setting, and particularly, what underlying dimensions may categorise the measures. We have extended and deepened this work in a new paper in Information Systems. We find three dimensions - Adhesion, Relevance, and Simplicity.

This paper was not edited by Robert Silverberg and we provide no guarantee of pulp Art Nouveau hallucinations.

The journal paper is A Chance For Models To Show Their Quality: Stochastic Process Model-Log Dimensions, and is co-authored with Sander Leemans, Moe Wynn, Wil van der Aalst and Arthur ter Hofstede. In it, we add:

  • Metrics for entropic relevance (Alkhammash et al) and alpha precision (Depaire et al), which were published after the initial paper
  • A second round of experiments and analysis
  • Candidate metrics based on the three dimensions
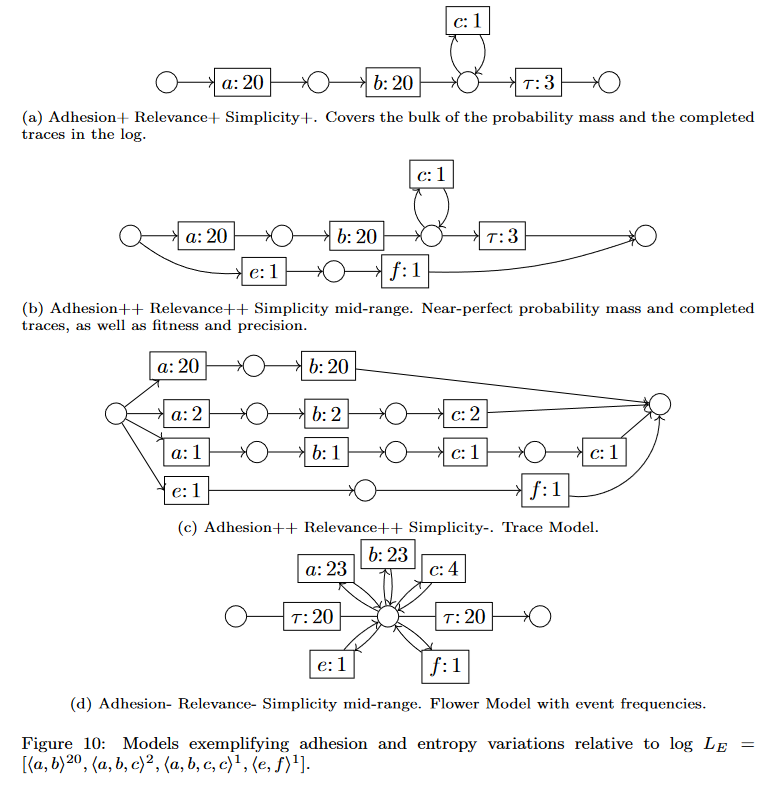
  • Detailed demonstrations of the dimensions in use on example models

Along the way we found a number of secondary results of technical interest, including:

  • More detail on our playout log solution to trace probability (Trace-Prob) (See Leemans, Maggi & Montali, 2022 for more on this problem)
  • An implementation of the entropic relevance measure using playout trace-prob which applies to any Petri net, and is not restricted to Stochastic Deterministic Finite Automata (SDFAs)
  • A variation on the alpha precision measure, existential precision, which allows easier comparison across domains, and an implementation of the same

Many thanks to the whole authorship team. The paper is published is an open access version and a pre-print, and we have also shared an open code repository.

References

Alkhammash, H., Polyvyanyy, A., Moffat, A., & García-Bañuelos, L. (2022). Entropic relevance: A mechanism for measuring stochastic process models discovered from event data. Information Systems, 107, 101922. https://doi.org/10.1016/j.is.2021.101922

Burke, A., Leemans, S. J. J., Wynn, M. T., van Der Aalst, W. M. P., & Hofstede, A. H. M. T. (2022). Stochastic Process Model-Log Quality Dimensions: An Experimental Study. International Conference on Process Mining.

Burke, A. T., Leemans, Sander J.J., Wynn, Moe T., van der Aalst, Wil M.P., ter Hofstede, Arthur H.M. A Chance For Models To Show Their Quality: Stochastic process model-log dimensions (2024). Information Systems, Volume 124, 2024, 102382.

Depaire, B., Janssenswillen, G., & Leemans, S. J. J. (2022). Alpha Precision: Estimating the Significant System Behavior in a Model. In C. Di Ciccio, R. Dijkman, A. del Río Ortega, & S. Rinderle-Ma (Eds.), Business Process Management Forum (pp. 120–136). Springer International Publishing. https://doi.org/10.1007/978-3-031-16171-1_8

Leemans, S. J. J., Maggi, F. M., & Montali, M. (2022). Reasoning on Labelled Petri Nets and Their Dynamics in a Stochastic Setting. In C. Di Ciccio, R. Dijkman, A. del Río Ortega, & S. Rinderle-Ma (Eds.), Business Process Management (pp. 324–342). Springer International Publishing. https://doi.org/10.1007/978-3-031-16103-2_22