Quality Dimensions For Stochastic Process Models
Process mining has a technical basis, but its purpose is describing behaviour. The behaviour it describes is not of a singular person, or an animal, but of a social organisation. Process mining uses process models in its descriptions - things like Petri nets - and in my own research, those models are stochastic. One important way to describe things scientifically is to use quantitative measures. What are the right measures to use? How do they relate to one another? Within the fairly focused area of stochastic process models, my recent paper takes a broad-brushed and empirical approach to these questions. I worked with a team of distinguished co-authors on this: Sander Leemans, Moe Wynn, Wil van der Aalst, and Arthur ter Hofstede.

Midjourney.
A desirable property in these circumstances is orthogonality: finding what elements vary independently of one another. At the current maturity of stochastic process mining, we are a little like a natural scientist from a previous era, walking into an unknown forest with a bag full of instruments. We are trying to take as many careful measuresments as we can, with our thermometers, barometers, microscopes, scales and astrolabes, but we don’t yet know how all of these measures relate to underlying physical forces. And of course it is complicated further by the fact we are studying organisations made up of both humans and machines.
Our approach was to generate a large number of models, of varying quality, using a variety of public logs (6). An additional challenge is that there are only a few existing stochastic process measures, and they are computationally expensive and/or restrictive (for example entropy-based measures require SDFAs). So we used a broad selection of 17 cheap exploratory measures, including 13 new measures created for this study. Usually these were cheaper versions of existing measures - for example a trace-wise version of the Earth-Movers’ Distance measure. In our analogy, this let us put a lot of instruments in our backpack, with the expectation there would be some overlap in the underlying properties they measured.
This gave us a lot of data, and with the use of a Principal Component Analysis, we saw evidence for three dimensions, which we name Adhesion, Entropy and Simplicity. Adhesion represents how little change is required to modify one process into another. Entropy and Simplicity dimensions are existing concepts and they pretty much do what they say on the tin.
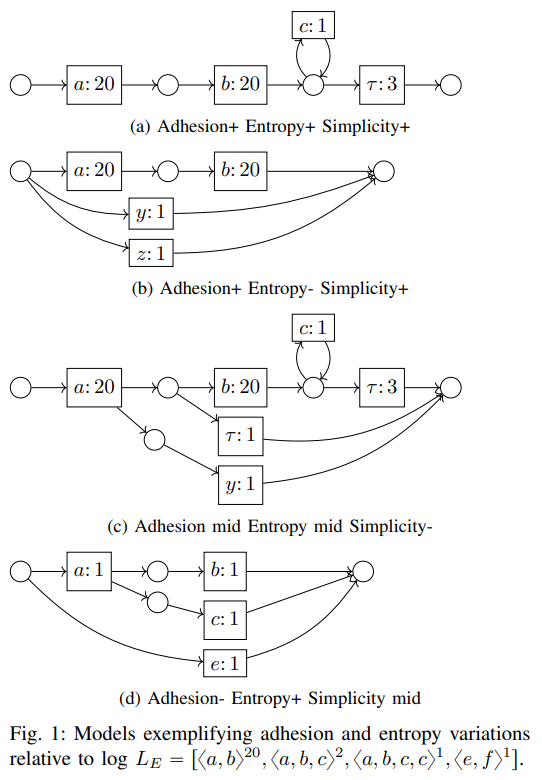
Along the way a certain amount of technical innovation was required, which people might also find useful:
- A genetic miner for discovering stochastic models, in the form of Probabilistic Process Trees
- A technique for generating playout logs from stochastic models, which many of the cheap exploratory measures exploit. A nice property of stochastic models is that by describing the behaviour more precisely in probabilistic terms, they make sampling-based playout less necessary: you already know the expected proportions.
- A calculation for trace probability (Trace-Prob) from those same stochastic playout logs. (See Leemans, Maggi & Montali, 2022 for more on this problem.)
This is an initial study which I think sets up a number of new directions to expand on and explore. Many thanks to Sander Leemans, who presented the paper at ICPM, and to the whole authorship team. It will be in the ICPM proceedings, but in the meantime, you can find a preprint here, and the slides here.
References
van der Aalst, W. (2016). Process Mining: Data Science in Action (2nd ed.). Springer-Verlag. https://doi.org/10.1007/978-3-662-49851-4
Burke, A., Leemans, S. J. J., Wynn, M. T., van Der Aalst, W. M. P., & Hofstede, A. H. M. T. (2022). Stochastic Process Model-Log Quality Dimensions: An Experimental Study. International Conference on Process Mining.
Leemans, S. J. J., Maggi, F. M., & Montali, M. (2022). Reasoning on Labelled Petri Nets and Their Dynamics in a Stochastic Setting. In C. Di Ciccio, R. Dijkman, A. del Río Ortega, & S. Rinderle-Ma (Eds.), Business Process Management (pp. 324–342). Springer International Publishing. https://doi.org/10.1007/978-3-031-16103-2_22