Toothpaste Miner
When we try to understand an organizational process, it’s interesting to know how often different things happen. Is an event rare, or routine, given previous events? Currently, in process mining, there are many techniques to discover causal relations in the form of control-flows. Frequencies or probabilities are usually added as later annotations, when they are considered at all. I have a new paper out with Sander Leemans and Moe Wynn, where probability is considered throughout the discovery process, directly producing a stochastic model as output. We call this framework the Toothpaste Miner.
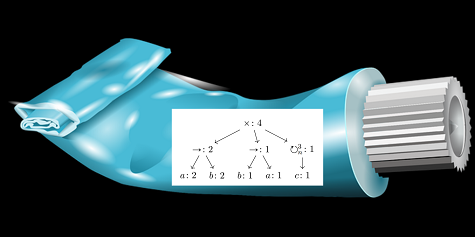
Process mining discovery proceeds from an event log to a process model. The basic idea with the Toothpaste miners is they start with a representation of the event log that preserves all of its causal and stochastic information. It then repeatedly applies transformation rules which reduce the size of the model. Rules are classified by how much information they preserve, and applied in order, preferring ones that preserve more information. In this way similar traces are consolidated into a model summary, like squeezing a part-empty tube of toothpaste. The internal model and final output is a Petri net variant called a Generalized Labelled Stochastic Petri Net. The data structural view on that Petri net is in the form of a weighted process tree.
We were able to show the algorithm terminates, preserves determinism where it is found, and runs in polynomial time. There’s also a prototype in Haskell which is restricted to binary trees and partial implementations of some rules. I presented the paper at Petri Nets 2021 a few weeks ago, and there’s a 180s teaser video, a 15 minute talk, and some slides, as well as a preprint of the paper itself.
References
Burke, A., Leemans, S. J. J., & Wynn, Moe Thandar. (2021). Discovering Stochastic Process Models By Reduction and Abstraction. International conference on applications and theory of Petri nets and concurrency.