One of the powerful things about Petri nets is they are both a mathematical formalism and a diagram. You can look at them and understand them in a different way from interpreting symbolic text. While there are a diversity of Petri net diagramming tools, when working as a developer with process mining tools, I found myself wanting something terse and text-based which still kept a diagrammatic aspect. I especially wanted something in this shape when I was doing testing. Hence, Petri net fragments.

PetriNetFragmentParser parser = new PetriNetFragmentParser();
StochasticNet net = parser.createNet("net",
                     "I -> [a] -> F");
parser.addToNet(net, "I -> [b] -> F");

This specifies the simple Petri net:
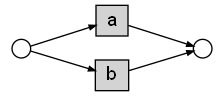
Single choice petri net

Transitions have brackets and places don’t. The -> is used for arcs.

The basic idea is that each line of text describes a path through the net. The resulting net is made of a union of those paths, but is also a full Petri net, so it isn’t restricted to just the originating traces. For example a loop can be specified by joining a place back to a line. Initial and final places are recognized by I and F naming conventions (and a few others like Start and End).

PetriNetFragmentParser parser = new PetriNetFragmentParser();
StochasticNet net = parser.createNet("net",
                     "I -> [a] -> p1 -> [b] -> F");
parser.addToNet(net,             "p1 -> [c] -> p1");

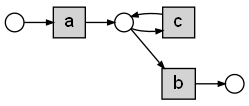
Petri net with looo

As stochastic models are a research interest of mine, transition weights are supported by using {transition weight} instead of [transition]. There is also support for duplicate labels. A full syntax is in here.

Start -> {registerrequest 1.0} -> p1 -> {examinethoroughly 1.0} -> p2
Start -> {registerrequest 1.0} -> p1 -> {examinecasually 10.0} -> p2
Start -> {registerrequest 1.0} -> p3 -> {checkticket 1.0} -> p4
p2 -> {decide 1.0} -> p5
p4 -> {decide 1.0} -> p5
p5 -> {paycompensation 1.0} -> End
p5 -> {rejectrequest 2.0} -> End
p5 -> {reinitiaterequest 1.0} -> p3

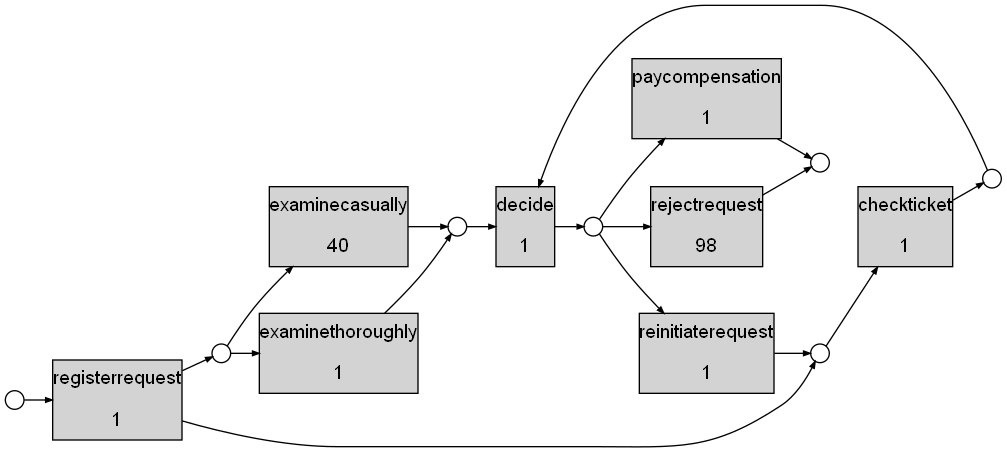
Airline compensation with weights

((This model is a slight extension of an airline compensation process example from p191 of the van der Aalst textbook Process Mining: Data Science in Action, which is a comprehensive technical overview of the topic.))

One current constraint is that space is used as a delimiter, and there’s no quotation for labels at the moment. If you want to improve on that, patches are always welcome.

A full syntax is here.

A second, simpler, utility, DelimitedTraceToXESConverter, creates XES XLog objects from delimited text. Each argument is a trace, and events are space-separated.

XLog log = converter.convertTextArgs("a a","a b","b","c");

The delimiters are configurable. These traces can also be read from a file, with one trace per line.

Petri net fragments and delimited text XLogs can then be combined together for clear, readable, process mining unit tests:

@Test
public void zeroMatch() {
    XLog log = converter.convertTextArgs("b c","b");
    AcceptingStochasticNet net = parser.createAcceptingNet("net", 
        "Start -> {a 2.0} -> End");
    assertMeasureEquals(0.0, log, net );
}

Functions for reading directly from a file are in PetrinetExportUtils. A small command line tool, PetriNetConverter, can be used to lay out Petri net diagrams declaratively, without resorting to a graphical editor, LaTeX tikz, or handcoding PNML. You can convert to DOT format and then use the usual DOT layout tools, which is how I created the images in this post.

usage: pnc [-i <arg>] [-o <arg>] [-v]
 -i,--input-format <arg>    Input format (PNML,FRAG)
 -o,--output-format <arg>   Output format (PNML,DOT)
 -v,--verbose               Verbose output.

Petri net fragments and the XES delimited text parser aren’t attempts to replace PNML, XES or DOT, which all serve their purposes as verbose, human-inspectable, interoperability standards. The intent is to optimize for the common case of tersely describing the key elements of a net in a developer-readable way.

I have bundled these tools together with a few other common Java utilties for process mining in the prom-helpers library. All ideas and feedback appreciated.

References

van der Aalst, W. (2016). Process Mining: Data Science in Action (2nd ed.). Springer-Verlag. https://doi.org/10.1007/978-3-662-49851-4